Nsakrty
算术平方根的快速估算
推理过程
\[\begin{array}{c} 众所周知,对于任意的一个实数x,都有其对应的\sqrt{x}的值\\ 设x_0=\left \lfloor \sqrt{x} \right \rfloor,x_1=\sqrt{x}-x_0\\ 则有x=(x_0+x_1)^2=x_0^2+2x_0x_1+x_1^2\\ 所以x\approx x_0^2+2x_0x_1\\ x_1\approx \frac{x-x_0^2}{2x_0}\\ \sqrt{x}\approx x_0+\frac{x-x_0^2}{2x_0}=\frac{x+x_0^2}{2x_0} \end{array}\]注:
- $\left \lfloor \sqrt{x} \right \rfloor$是这个数的算术平方根的整数部分,很容易推出,
- $\sqrt{x}-x_0$是这个数的算术平方根的小数部分
与实际值的误差的图像
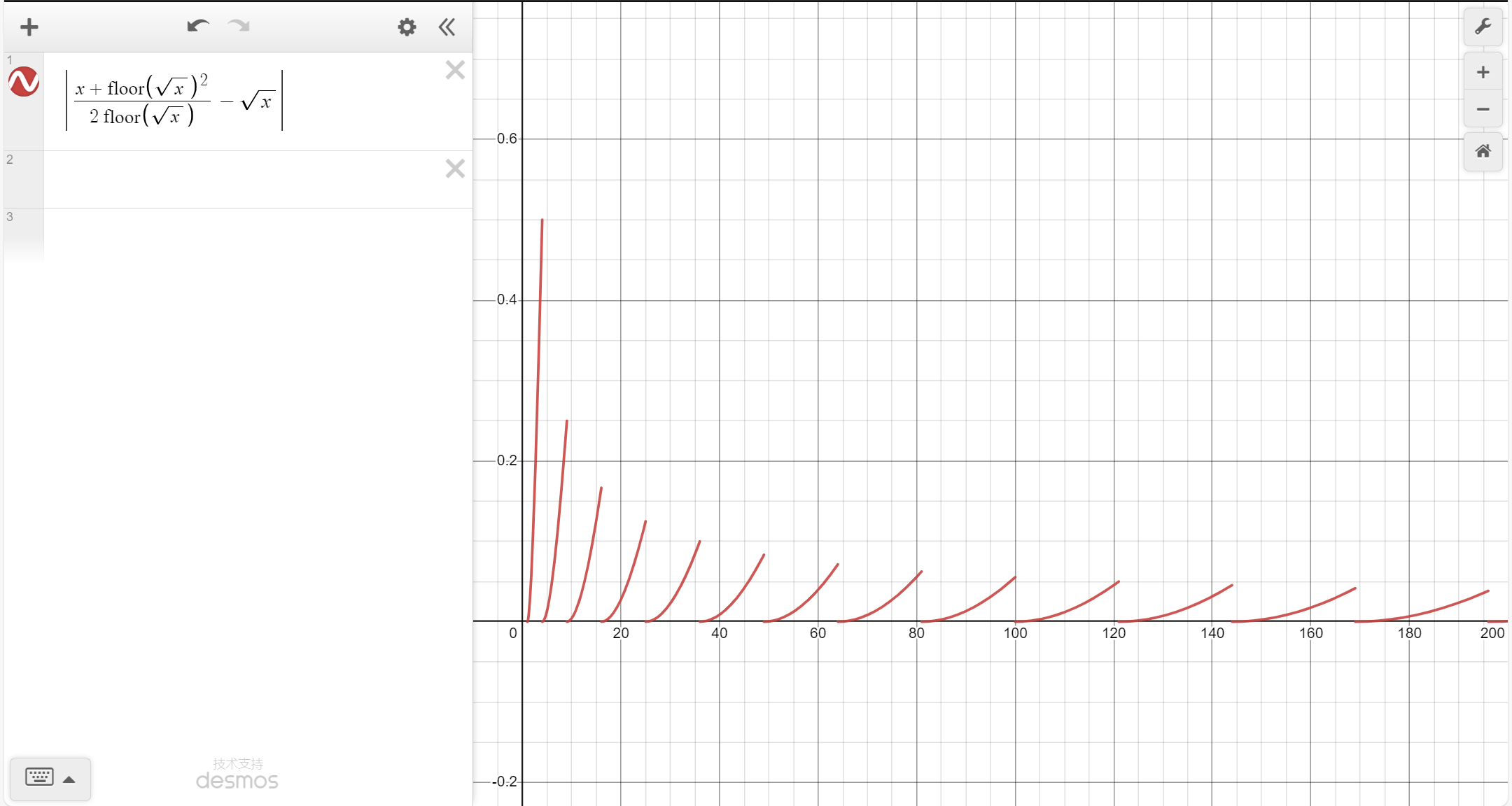
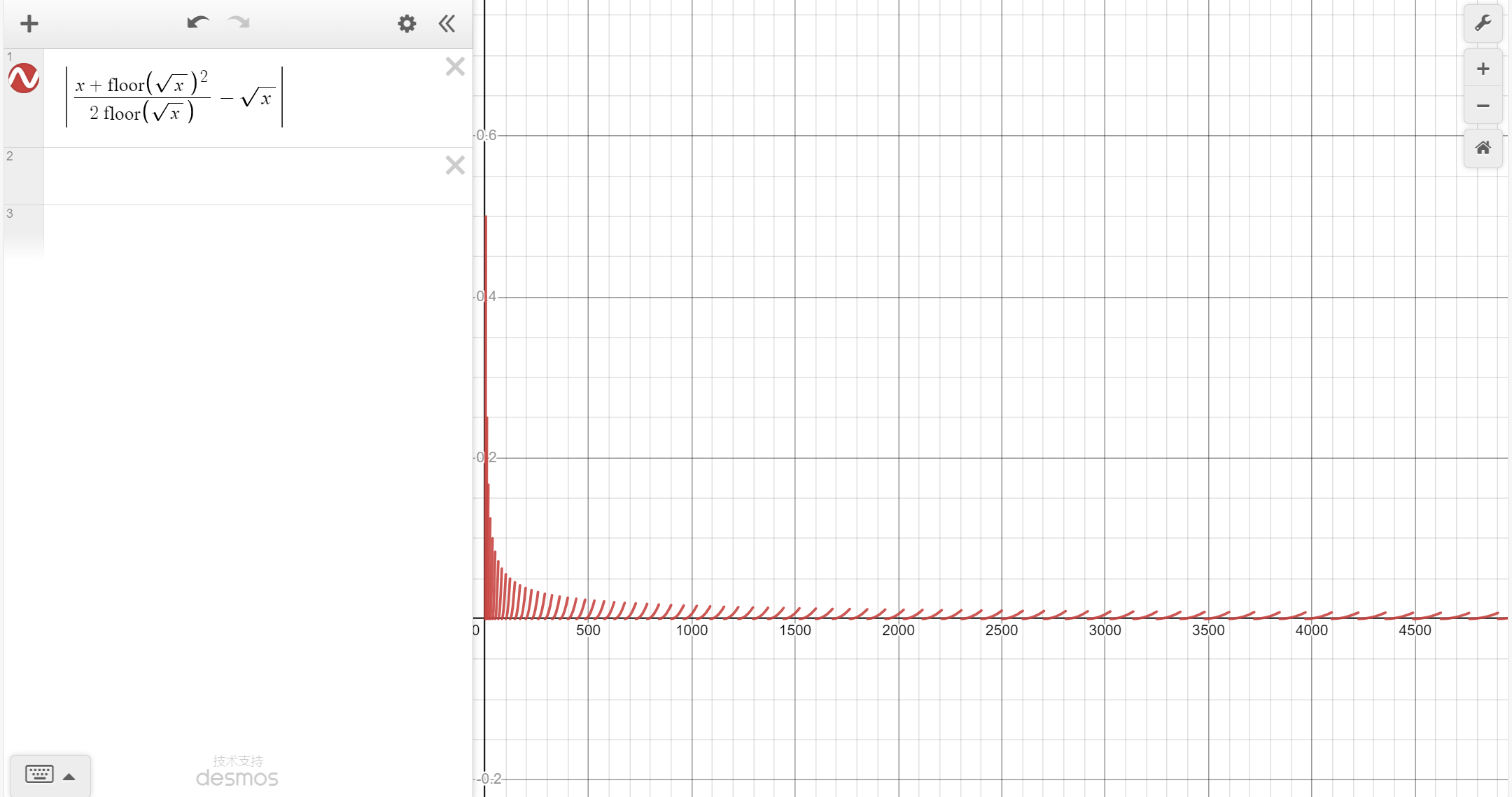
如何减小误差
由图像可知, $x$ 的值取得越大,误差越小。
因为一个数的 $100$ 倍的算术平方根等于这个数的算术平方根的 $10$ 倍,所以我们使用此方法减小误差时可以选择把数字乘上 $100$ ,再使用此方法,最后再将结果除以 $10$ ,即可得到更精确的算术平方根,如果想取得更精确的位数,请乘上 $100^x$ ,再把结果除以 $10^x$ 即可,其中 $x$ 是整数。
三个示例
$\sqrt{2} \approx \frac{2+1^2}{2*1} = 1.5$
$\sqrt{200} \approx \frac{200+14^2}{2*14} \approx 14.14$
$\sqrt{114514} \approx \frac{114514+338^2}{2*338} \approx 338.3994$
可以看到非常的好(垃)用(圾)XD